1、求根公式是什么？

求根公式为：

ax²+bx+c=0,a≠0

x1=[-b-√(b²-4ac)]/(2a)

x2=[-b+√(b²-4ac)]/(2a)

韦达定理为：

x1+x2=-b/a

x1*x2=c/a

发展历史：

法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中改进了三、四次方程的解法，还对n=2、3的情形，建立了方程根与系数之间的关系，现代称之为韦达定理。

韦达最早发现代数方程的根与系数之间有这种关系，因此，人们把这个关系称为韦达定理。韦达在16世纪就得出这个定理，证明这个定理要依靠代数基本定理，而代数基本定理却是在1799年才由高斯作出第一个实质性的论性。

2、方程的根求解公式

求根公式如下：

a为二次项系数，b为一次项系数，c是常数。

一元二次ax^2 +bx+c=0可用求根公式x= 求解，它是由方程系数直接把根表示出来的公式。这个公式早在公元9世纪由中亚细亚的阿尔·花拉子模给出。

拓展知识：

虽然阿拉伯人在九世纪，就掌握了求解一元二次方程的方法。

但一元二次方程最为重要的理论，是由法国数学家韦达建立的，他在《论方程的识别与订正》中讨论了根和方程的系数之间的关系，这一重要结果也被命名为韦达定理。

一元二次方程的求根公式

要讨论任意方程的性质，首先我们需要一个对所有方程都能使用的解法。

对于一元二次方程，我们只需要先把对应的二次函数一般式转化成顶点式，再开平方求解：

其中Δ决定了方程能否顺利完成开平方的运算，被称为根的判别式。

如果Δ>0，那么我们就能顺利开平方，计算出x的两个解，也可以叫两个根。

而如果Δ<0，我们不能对负数开平方，方程在实数范围内无解。

特别地，Δ=0时，我们说方程的两个解大小一样，叫做重根。

韦达定理的逆定理

如果我们有一元二次方程，可以通过韦达定理求出两个根的和与乘积。

那么反过来，如果我们知道两个根的和与乘积，就可以构造出对应的一元二次方程并求解。

人们思考高次多项式是否和二次多项式之间有某种联系。

对于有n个根的n次有理多项式，一定能因式分解为一堆一次或二次有理多项式的乘积，即一个有理根对应一个一次多项式，一对无理根对应一个二次多项式。

进一步利用复数解决无实根的情况，可以证明，n次多项式一定能因式分解为一堆一次或二次多项式的乘积，即一个实根对应一个一次多项式，一对复根对应一个二次多项式。

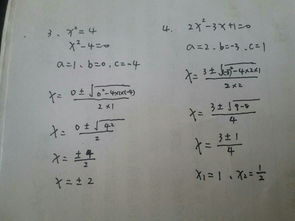
3、求根公式

公式法求根公式如下：

求根公式指的是，一元二次（或多次）的方程程序化得出的的求根计算公式，一元二次ax^2+bx+C=0可用求根公式x=（-b±V（b^2-4ac）/2a，a为二次项系数，b为一次项系数，C是常数，它是由方程系数直接把根表示出来的公式。

公式法（是解一元二次方程的方法，根据因式分解与整式乘法的关系，把各项系数直接带入求根公式，可避免配方过程而直接得出根的方法。

4、求根公式

求根公式：x={-b（b2-4ac）}/（2a）。

所谓方程的根是方程左右两边相等的未知数的取值。一元二次方程根和解不同，根可以相同，而解一定是不同的。

公式就是用数学符号表示各个量之间的一定关系（如定律或定理）的式子。具有普遍性，适合于同类关系的所有问题。在数理逻辑中，公式是表达命题的形式语法对象，除了这个命题可能依赖于这个公式的自由变量的值之外。

这个公式包括了初中阶段所学过的全部运算：加、减、乘除、乘方、开方。其中，除法要求分母不为零，这个是满足的。

但是开平方要求被开方数非负，这个要求并不一定总能满足，基于这个原因就导致了有的方程有实数根，有的方程没有实数根。这一个公式里面包含六种运算，在整个初中阶段，仅此一个。

学习数学重要性：

1、数学与我们生活息息相关。要说学数学的真正效果，它不是体现在应试教育上，而是将来自身的思维上。

2、数学的重要性不言而喻。数学是一切科学的基础，是培养逻辑思维重要渠道，可以说我们人类的每一次重大进步都有数学这门学科在做强有力的支撑。

3、生活中的数学知识运用无处不在。从日常生活中柴米油盐的费用的计算，到天文地理、质量控制、农业经济、航天事业都存在着运用数学的影子。

请添加微信号咨询：19071507959

在线报名

上一篇：求斜率,求斜率的公式是什么

下一篇：求爱信,情人节求爱短信大全