1、总体均值的区间估计公式

总体均值的区间估计公式是：SX±Z（1-α）√n。

统计学中，在研究某一特征的均值时，我们无法确定真实的均值，只能通过样本中的均值来对整体均值进行预测。区间估计是了解样本统计量中真实值的一个方法，其中所估计的范围反映出了统计量估计真实参数的不确定性。总体均值的区间估计公式是一种用来估计总体均值的区间估计方法。

1、区间估计的概念

区间估计是统计学中一项基本的推论方法，指在估计总体特征时将各个样本的数据用来估计总体的特征，并将估计误差控制在一定的范围内。区间估计方法可以明确地表达估计值的置信度以及超过该置信度的置信水平。

2、区间估计的优点

相对于点估计，区间估计具有更强的研究意义，能够全面地反映出数据的变化情况。并且，区间估计也可以在一定程度上减少由于样本数据的偏差而引起的误差。

3、区间估计的公式

总体均值的区间估计公式通常采用t分布和Z分布进行计算。如果总体标准差已知，则应采用Z分布计算，而如果总体标准差未知，则应选择t分布计算。 其中，

- 若Z分布，[µ- Z(α/2) * (σ/√n), µ + Z(α/2) * (σ/√n)]；

- 若t分布，[µ- t(α/2, n-1) * (s/√n), µ + t(α/2, n-1) * (s/√n)]

其中µ表示总体均值，α表示置信水平，Z(α/2)或t(α/2,n-1)是分布表中相应的z标准分或t标准分，该值可由信心水平和自由度确定；σ（或s）是总体（或样本）的标准差，n是样本容量大小。

区间估计的重要性

区间估计是统计学中重要的思想和方法，可以帮助研究者全面了解数据变化情况，计算出真实的参数估计值，并尽可能降低数据偏差以及误差的出现。 然而，由于数据及各种不确定因素的存在，估计结果仍然只是一个范围，不能精确确定一个点值。在实际应用中，应当根据实际情况选择合适的分布和方法，以尽可能准确地估计出参数的区间范围。

2、什么是“点估计”和“区间估计”？两者的主要区别是什么？

点估计:是利用根本的样本数据，对未知的参数进行估计所得到的一个具体的数据。

区间估计:是通过根本的样本数据，估计未知参数，在可信度下的最可能的存在区间中得到的结果，结果是一个区间。

两者最大的区别:点估计就是估计一个具体的数值，区间估计就是估计一段区间。

点估计也被称定值估计，点估计是以抽样得到的样本指标作为总体指标的估计量，并且以样本指标的实际值直接作为总体未知参数的估计值的一种推断方法。是参数估计的一种形式。通过从总体中抽取的样本，根据一定的正确度与精确度的要求，构造出适当的区间，以作为总体的分布参数的真值所在范围的估计。

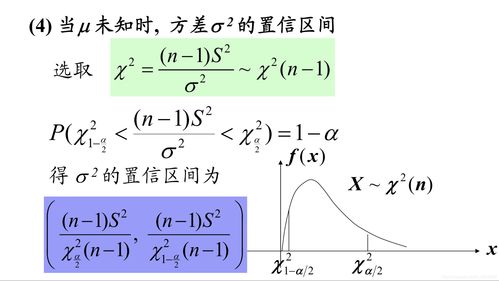
3、什么是点估计和区间估计？两者的主要区别是什么？

1、含义

点估计（point estimation）是用样本统计量来估计总体参数，因为样本统计量为数轴上某一点值，估计的结果也以一个点的数值表示，所以称为点估计。

区间估计（interval estimate）是在点估计的基础上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。

2、两者主要区别

（1）值不同

点估计的精确程度用置信区间表示。由样本数据估计总体分布所含未知参数的真值，所得到的值，称为估计值。

区间估计，是参数估计的一种形式。通过从总体中抽取的样本，根据一定的正确度与精确度的要求，构造出适当的区间，以作为总体的分布参数(或参数的函数)的真值所在范围的估计。

（2）是否考虑抽样误差

点估计是在抽样推断中不考虑抽样误差，直接以抽样指标代替全体指标的一种推断方法。因为个别样本的抽样指标不等于全体指标，所以，用抽样指标直接代替全体指标，不可避免的会有误差。

区间估计是抽样推断中根据抽样指标和抽样误差去估计全体指标的可能范围的一种推断方法。在从抽样指标推断全体指标时，用一定概率保证误差不超出某一给定范围。

（3）常用方法不同

点估计的常用方法有矩估计法、顺序统计量法、最大似然法、最小二乘法等。

区间估计求置信区间的方法，最常用的求置信区间及置信上、下限的方法有利用已知的抽样分布（见统计量）、利用区间估计与假设检验的联系、利用大样本理论（见大样本统计）、

来源：

百度百科-定估计与区间估计

百度百科-点估计

百度百科-区间估计

4、概率论的区间估计怎么理解？

区间估计就是以一定的概率保证估计包含总体参数的一个值域，即根据样本指标和抽样平均误差推断总体指标的可能范围。它包括两部分内容：一是这一可能范围的大小；二是总体指标落在这个可能范围内的概率。区间估计既说清估计结果的准确程度，又同时表明这个估计结果的可靠程度，所以区间估计是比较科学的。

请添加微信号咨询：19071507959

在线报名

上一篇：区间,什么是区间

下一篇：匿,匿怎么读什么意思