1、如何求导数

求导数方法如下：

第一步：确定函数的定义域．如本题函数的定义域为R。

第二步：求f（x）的导数f′（x）。

第三步：求方程f′（x）＝0的根。

第四步：利用f′（x）＝0的根和不可导点的x的值从小到大顺次将定义域分成若干个小开区间，并列出表格。

第五步：由f′（x）在小开区间内的正、负值判断f（x）在小开区间内的单调性。

第六步：明确规范地表述结论。

第七步：反思回顾。查看关键点、易错点及解题规范。

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f\'（x0）或df（x0）/dx。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

2、怎么求导数啊？

如下图所示。

常用导数公式：

1、y=c(c为常数) y\'=0

2、y=x^n y\'=nx^(n-1)

3、y=a^x y\'=a^xlna，y=e^x y\'=e^x

4、y=logax y\'=logae/x，y=lnx y\'=1/x

5、y=sinx y\'=cosx

6、y=cosx y\'=-sinx

7、y=tanx y\'=1/cos^2x

8、y=cotx y\'=-1/sin^2x

9、y=arcsinx y\'=1/√1-x^2

导数的求导法则

由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。基本的求导法则如下：

1、求导的线性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合（即①式）。

2、两个函数的乘积的导函数：一导乘二+一乘二导（即②式）。

3、两个函数的商的导函数也是一个分式：（子导乘母-子乘母导）除以母平方（即③式）。

4、如果有复合函数，则用链式法则求导。

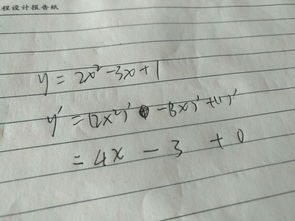
3、如何求导数，求导的公式是什么？

以下是18个基本导数公式（y：原函数；y\'：导函数）：

1、y=c，y=0（c为常数）

2、y=xxμ，y\'=μxμ负1（μ为常数且μ不等于0）。

3。y=aAx，y\'=aAxIna。y=eAx，y\'=eAx。

4、y=logax，y\'=1/（xina）（a>0且a=1）；y=Inx，y\'=1/x。

5、y=sinx，y\'=cosx。

6、y=cosx，y\'=负sinx。

7、y=tanx，y\'=（secx）2=1/（cosx）2。

8、y=cotx，y\'=负（cscx）2=负1/（sinx）2。

9、y=arcsinx，y\'=1/√（1负x2）。

10、y=arccosx，y\'=负1/√（1负x2）。

11、y=arctanx，y\'=1/（1+x2）。

12、y=arccotx，y\'=负1/（1+2）。

13、y=shx，y\'=chx。

14、y=chx，y\'=shx。

15、y=thx，y\'=1/（chx）2。

16、y=arshx，y\'=1/V（1+x12）。

17、y=c（c为常数）y\'=0

18、y=xny\'=nxx（n负1）。

4、求导方法总结全部

求导方法总结全部内容如下：

从导数与微分的关系可知，会求导数，就一定会求微分。

y=f(x),dy=f\'(x)dx,dy/dx=f\'(x)。

导数的计算方法一般以下分为8种情形：

1.公式法：这个方法需要熟练掌握导数的基本公式。

2.导数四则运算公式：导数的乘法和除法公式要能熟练运用。

3.复合函数的链式法则--非常重要的求导方法。

链式法则在应用时一般分成4步：分解-各自求导-相乘-回代。

如果计算熟练，可以不设中间变量，直接求复合函数的导数。

4.反函数求导法：

利用这种方法求导时，要注意：先取反函数，然后对反函数 siny 求导，特别注意此时y是自变量，所以 siny 的导数是 cosy。

5.对数求导法：

一般两种情况会使用对数求导法，这两种情况都是对等式两端同时取自然对数，利用对数的运算性质对函数进行变形。

求幂指函数的导数。

求复杂根式的导数：

6.隐函数求导法：隐函数是隐藏在一个方程中的函数，要用到链式法则。

7.参数方程求导法：注意参数方程求导公式。

dy/dx=y\'t/x\'t。

8.高阶导数：

下面这个例子是一个求高阶导数的经典例题。一般求二阶导数要多练习求隐函数和参数方程的二阶导数。

请添加微信号咨询：19071507959

在线报名

上一篇：求导公式表,基本求导公式表

下一篇：求导符号,导数符号