1、莫比乌斯带是什么意思？

莫比乌斯带也叫莫比乌斯环；是天文学家莫比乌斯和约翰•李斯丁在1858年独立发现的。这个结构很简单，用一个纸带旋转半圈再把两端粘上后就行了。

莫比乌斯环很奇妙，原先纸带有两个面，而它只有一个面。沿着原先莫比乌斯环中间剪开，将会形成一个比原先莫比乌斯环大一倍，具有正反两面的环，而不是形成两个莫比乌斯环或其他形式的环。

此外，莫比乌斯环在数学中是一种拓扑学结构，在空间，边界证明中有重要的作用。

2、莫比乌斯带的由来是什么？

莫比乌斯带的由来：

公元1858年，德国数学家莫比乌斯（Mobius，1790～1868）和约翰·李斯丁发现：把一根纸条扭转180°后，两头再粘接起来做成的纸带圈，具有魔术般的性质。

普通纸带具有两个面（即双侧曲面），一个正面，一个反面，两个面可以涂成不同的颜色；而这样的纸带只有一个面（即单侧曲面），一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”（也就是说，它的曲面从两个减少到只有一个）。

拓扑变换

莫比乌斯带是一种拓展图形，它们在图形被弯曲、拉大、缩小或任意的变形下保持不变，只要在变形过程中不使原来不同的点重合为同一个点，又不产生新点。换句话说，这种变换的条件是：在原来图形的点与变换了图形的点之间存在着一一对应的关系，并且邻近的点还是邻近的点。这样的变换叫做拓扑变换。

拓扑有一个形象说法——橡皮几何学。因为如果图形都是用橡皮做成的，就能把许多图形进行拓扑变换。例如一个橡皮圈能变形成一个圆圈或一个方圈。但是一个橡皮圈不能由拓扑变换成为一个阿拉伯数字8。因为不把圈上的两个点重合在一起，圈就不会变成8，“莫比乌斯带”正好满足了上述要求。

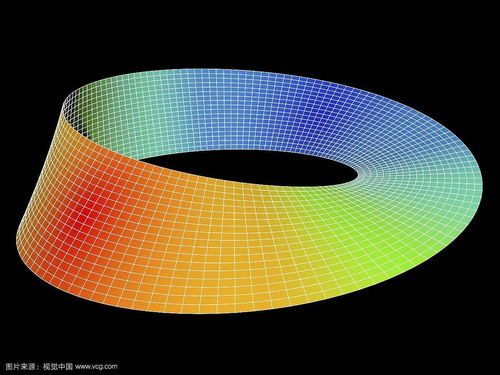
3、莫比乌斯带原理是什么

莫比乌斯带的原理是普通纸带的两个面（即双侧曲面），正面与反面涂成不同的颜色把这个纸带变成一个面（即单侧曲面），一只小虫爬遍整个曲面而不必跨过它的边缘。

这种纸带被称为“莫比乌斯带”（也就是说，它的曲面只有一个）。

莫比乌斯带解析：

莫比乌斯带是一种拓展图形，它们在图形被弯曲、拉大、缩小或任意的变形下保持不变，只要在变形过程中不使原来不同的点重合为同一个点，又不产生新点。

在普通空间无法实现的＂手套易位＂问题。

人左右两手的手套虽然极为相像，但却有着本质的不同。

我们不可能把左手的手套贴切地戴到右手上去；也不能把右手的手套贴切地戴到左手上来。

无论你怎么扭来转去，左手套永远是左手套，右手套也永远是右手套。

但是倘若你把它搬到莫比乌斯带上来，那么解决起来就易如反掌了。

4、默比乌斯带怎么做？

【莫比乌斯带】的制作非常简单。只需要“把一条纸带，扭转180度，首尾粘连”，就完成了。

【莫比乌斯带】是德国数学家莫比乌斯，在1858年发现的。莫比乌斯带只拥有一个面，即单侧曲面。而不扭转的普通纸带则是拥有两个面，即双侧曲面。而单侧曲面拥有，一次性可以通过整个曲面而不必跨过其边缘的特性。

在现实生产生活中也是具有实际应用的，莫比乌斯带外形的传动皮带，不会只磨损一个面，而是皮带2面都能均匀使用磨损，提高了传动皮带的耐磨性，延长了皮带的使用寿命。

而且，莫比乌斯带还拥有其他特性。当莫比乌斯带被不同等分下剪开，会出现各种新的结构。

2等分。从正中间剪开，会形成一个比原来周长大1倍的新的莫比乌斯带。而一般的纸带从中间剪开，只会被分成2个独立的环带。

3等分。按3等分剪开，会形成一个比原来周长大1倍的新的莫比乌斯带和一个原长的嵌套莫比乌斯带。而一般的纸带3等分剪开，只会被分成3个独立的环带。

莫比乌斯带的发现，总结了大量的莫比乌斯带规律和数学公式，促使拓扑学有了长足的发展。也为现实生产生活中的应用提供了数学基础，比如传动皮带使用效率的提高，橡胶老化的降低，打印机色带的延寿。

请添加微信号咨询：19071507959

在线报名

上一篇：莫比乌斯带,莫比乌斯带是什么意思？

下一篇：莫焕晶9月21日枪毙,莫焕晶死了吗