1、菱形的判定方法4条

菱形的判定方法如下:

邻边相等的平行四边形

对角线相互垂直平行四边形

对角线各自平分一组对角

矩形的判定方法:

对角线相等的平行四边形

有一个角为直角的平行四边形

正方形的判定方法:

①对角线相互垂直;

②对角线相等;

③有一个角为直角;

④有一组邻边相等;

（以上任意选取两个条件）的平行四边形为正方形

菱形的定义：一组邻边相等的平行四边形叫做菱形。

菱形的性质：

1、对角线互相垂直且平分；

2、四条边都相等；

3、对角相等，邻角互补；

4、每条对角线平分一组对角；

5、菱形既是轴对称图形，对称轴是两条对角线所在直线，也是中心对称图形；

6、在60度的菱形中，短对角线等于边长，长对角线是短对角线的根号3倍；

7、菱形具备平行四边形的一切性质。

菱形特点是：

菱形具有平行四边形的一切性质。

菱形的四条边都相等。

菱形的对角线互相垂直平分且平分每一组对角。

菱形是轴对称图形，对称轴有2条，即两条对角线所在直线。

菱形是中心对称图形。

特殊定理：

1、具有平行四边形的性质。

2、菱形的四条边相等。

3、菱形的对角线互相垂直，并且每一条对角线平分一组对角。

4、菱形是轴对称图形，它有两条对称轴。（特殊的菱形-正方形有4条对称轴）

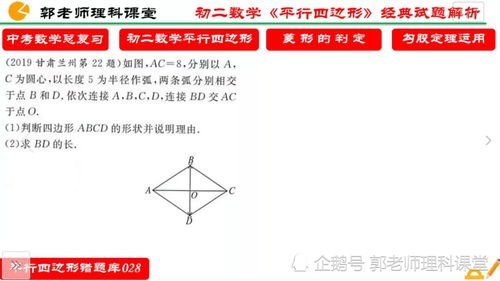
2、菱形的判定方法5个

菱形的5个判定方法如下：

一、四条边都相等的四边形是菱形。

二、有一组邻边相等的平行四边形是菱形。

三、对角线互相垂直的平行四边形是菱形。

四、对角线互相垂直且平分的四边形是菱形。

五、有一条对角线平分一组对角的平行四边形是菱形。

更加常用的判定方法其实只有以下三种：

1、四条边都相等的四边形是菱形。

2、对角线相互垂直的平行四边形是菱形。

3、有一组邻边相等的平行四边形是菱形。

并且菱形是在平行四边形的前提下定义的，它是一个平行四边形，而且是一个特殊的平行四边形，所以也可以说菱形是一个特殊的平行四边形。

：

平行四边形的判定：

1:有两组对边分别相等的四边形是平行四边形

2:两组对边分别平行的四边形是平行四边形

3:一组对边平行且相等的四边形是平行四边形

4：对角线互相平分的四边形是平行四边形

5：对角线相等的四边形是平行四边形

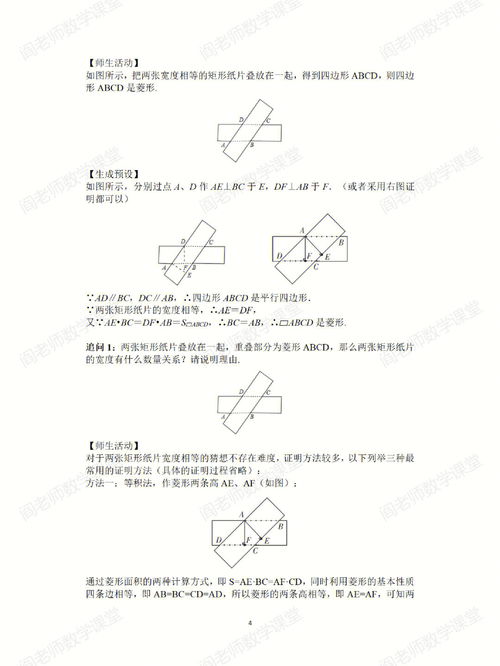
3、菱形的判定是什么？

菱形的判定是：有一组邻边相等的平行四边形叫做菱形。在同一平面内，有一组邻边相等的平行四边形是菱形，四边都相等的四边形是菱形，菱形的对角线互相垂直平分且平分每一组对角，菱形是轴对称图形，对称轴有2条，即两条对角线所在直线，菱形是中心对称图形。菱形是特殊的平行四边形之一。有一组邻边相等的平行四边形称为菱形。

菱形的判定定理：

1、菱形的对边平行，四条边都相等。

2、菱形的对角相等。

3、菱形的对角线互相垂直平分，并且每一条对角线平分一组对角。

4.四边都相等的四边形是菱形。

5.对角线互相垂直的平行四边形是菱形。

4、菱形的判定条件是什么？

菱形的判定条件：

1、一组邻边相等的平行四边形是菱形；

2、对角线互相垂直的平行四边形是菱形；

3、四条边均相等的四边形是菱形；

4、菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。

在一个平面内，有一组邻边相等的平行四边形是菱形。

菱形的性质：

1、菱形具有平行四边形的一切性质；

2、菱形的四条边都相等；

3、菱形的对角线互相垂直平分且平分每一组对角

4、菱形是轴对称图形，对称轴有2条，即两条对角线所在直线，菱形还是中心对称图形

5、菱形的面积等于两条对角线乘积的一半；当不易求出对角线长时，就用平行四边形面积的一般计算方法计算菱形面积S=底×高

菱形：

请添加微信号咨询：19071507959

在线报名

上一篇：菱形对角线,菱形的对角线有什么性质

下一篇：菱形的定义,什么是菱形概念