1、什么是菱形概念

有一组邻边相等的平行四边形叫做菱形；四边相等的四边形是菱形；对角线互相垂直且互相平分的平行四边形是菱形.

定义

菱形（rhombus）是特殊的平行四边形之一。有一组邻边相等的平行四边形称为菱形。如图1，在平行四边形ABCD中，若AB=BC，则称这个平行四边形ABCD是菱形，记作◇ABCD，读作菱形ABCD。

性质：

菱形具有平行四边形的一切性质；

菱形的四条边都相等；

菱形的对角线互相垂直平分且平分每一组对角；

菱形是轴对称图形，对称轴有2条，即两条对角线所在直线；

菱形是中心对称图形；

判定：

在同一平面内，一组邻边相等的平行四边形是菱形

对角线互相垂直的平行四边形是菱形；

四条边相等的四边形是菱形；

对角线互相垂直平分的四边形；

两条对角线分别平分每组对角的四边形；

有一对角线平分一个内角的平行四边形；

菱形是在平行四边形的前提下定义的，首先它是平行四边形，而且是特殊的平行四边形，特殊之处就是“有一组邻边相等”，因而增加了一些特殊的性质和判定方法。

菱形的一条对角线必须与x轴平行，另一条对角线与y轴平行。不满足此条件的几何学菱形在计算机图形学上被视作一般四边形。

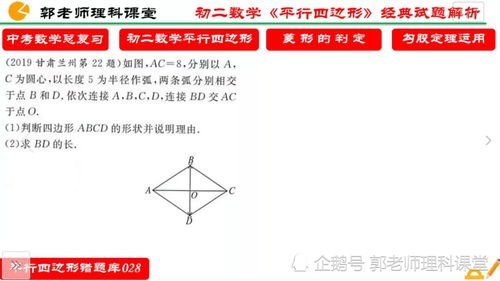
2、菱形的定义

题库内容：

菱形的解释

[diamond; lozenge; rhombus]

由四条相等的直线构造两个锐角和两个钝角组成的四边形 详细解释 平面上四边相等的四边形。它的对角线互相垂直平分，它的面积等于两对角线长度的乘积的一半。 韩北屏 《酋长的故事》 ：“他坐在‘客厅’正当中的一张木躺椅上，椅子的上端有一个牛皮做的菱形枕头。”

词语分解

菱的解释 菱 í 一年生水生草本植物，果实有硬壳，有角，称“菱”或“菱角”，可食。 部首 ：艹； 形的解释 形 í 实体：形仪（体态仪表）。 形体 。形貌。 形容 。形骸。形单影只。 形影相吊 。 样子：形状。形式。形态。形迹。地形。情形。 表现：形诸笔墨。喜形于色。 对照，比较： 相形见绌 。 状况，地势： 形势 。

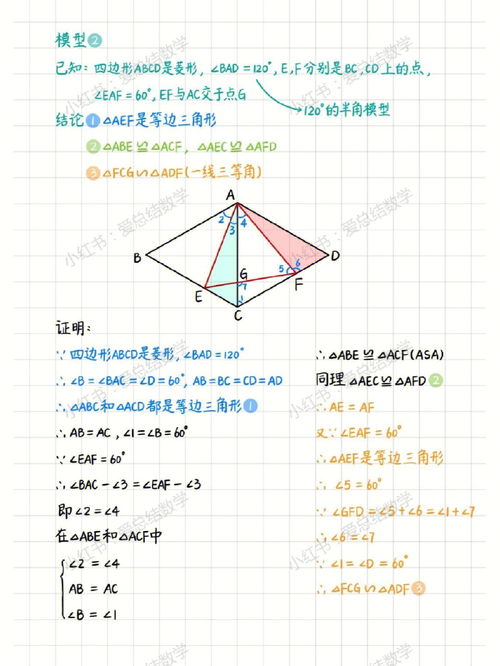
3、菱形的定义性质与判定

一、菱形的定义：一组邻边相等的平行四边形叫做菱形。

二、菱形的性质：1、对角线互相垂直且平分；2、四条边都相等；3、对角相等，邻角互补；4、每条对角线平分一组对角；5、菱形既是轴对称图形，对称轴是两条对角线所在直线，也是中心对称图形；6、在60度的菱形中，短对角线等于边长，长对角线是短对角线的根号3倍；7、菱形具备平行四边形的一切性质。

三、菱形的判定：1、一组邻边相等的平行四边形是菱形；2、四边相等的四边形是菱形；3、关于两条对角线都成轴对称的四边形是菱形；4、对角线互相垂直且平分的四边形是菱形。

4、什么是菱形的定义

菱形的定义：

在同一平面内，有一组邻边相等的平行四边形是菱形，四边都相等的四边形是菱形，菱形的对角线互相垂直平分且平分每一组对角，菱形是轴对称图形，对称轴有2条，即两条对角线所在直线，菱形是中心对称图形。

正方形

正方形，是特殊的平行四边形之一。即有一组邻边相等，并且有一个角是直角的平行四边形称为正方形，又称正四边形。正方形，具有矩形和菱形的全部特性。

矩形

有一个角是直角的平行四边形是矩形。矩形是一种特殊的平行四边形，正方形是特殊的矩形。

菱形

在同一平面内，有一组邻边相等的平行四边形是菱形，四边都相等的四边形是菱形，菱形的对角线互相垂直平分且平分每一组对角，菱形是轴对称图形，对称轴有2条，即两条对角线所在直线，菱形是中心对称图形。

梯形

梯形（trapezoid）是只有一组对边平行的四边形。平行的两边叫做梯形的底边：较长的一条底边叫下底，较短的一条底边叫上底；另外两边叫腰；夹在两底之间的垂线段叫梯形的高。一腰垂直于底的梯形叫直角梯形（right trapezoid）。两腰相等的梯形叫等腰梯形（isosceles trapezoid）。

性质

1.菱形具有平行四边形的一切性质；

2.菱形的四条边都相等；

3.菱形的对角线互相垂直平分且平分每一组对角；

4.菱形是轴对称图形，对称轴有2条，即两条对角线所在直线；

5.菱形是中心对称图形。

判定

在同一平面内：

1.一组邻边相等的平行四边形是菱形；

2.对角线互相垂直的平行四边形是菱形；

3.四条边相等的四边形是菱形；

4.对角线互相垂直平分的四边形；

5.两条对角线分别平分每组对角的四边形；

6.有一对角线平分一个内角的平行四边形；

请添加微信号咨询：19071507959

在线报名

上一篇：菱形的判定,菱形的判定方法4条

下一篇：菱形的性质,菱形有哪些性质